ஆய்லர் வரைபடம்

ஆய்லர் வரைபடம் (Euler diagram) என்பது கணங்களையும் அவற்றின் உறவுகளையும் குறிக்கும் ஒரு வரைபட வழிமுறையாகும். குறிப்பாக, இது சிக்கலான படிநிலைகளையும், ஒன்றுடனொன்று மேற்கவிந்த வரையறைகளை விளக்குவதற்கு பயன்படுகிறது. இவ்வரைபடங்களும் கணங்களின் மற்றொரு வரைபட நுட்பமான வென் வரைபடங்கள் போன்றவையே. வெவ்வேறு கணங்களுக்கு இடையிலான அனைத்து சாத்தியமான உறவுகளையும் காட்டும் வென் வரைபடங்களைப் போலல்லாமல், ஆய்லர் வரைபடங்கள் பொருத்தமான உறவுகளை மட்டுமே காட்டுகின்றன.

முதன்முதலில் சுவிட்சார்லாந்து நாட்டுக் கணிதவியலாளர் லியோனார்டு ஆய்லர் (1707-1783) என்பவரால் "ஆய்லேரிய வட்டங்கள்" பயன்படுத்தப்பட்டது. அமெரிக்காவில், வென் வரைபடங்களும் ஆய்லர் வரைபடங்களும் 1960 களின் புதிய கணித இயக்கத்தின் ஒரு பகுதியாக கணக் கோட்பாட்டில் இணைக்கப்பட்டன. அதன் பின்னர் இவ் வரைபடங்கள் வாசிப்பு, நிறுவனங்கள் மற்றும் வணிகத்துறை போன்ற பிற பாடத்திட்டத் துறைகளிலும் ஏற்றுக்கொள்ளப்பட்டுள்ளன.^[1]

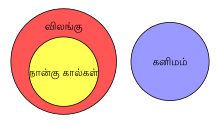
ஆய்லர் வரைபடங்கள் இரு பரிமாண தளத்தில் எளிமையான மூடிய வடிவங்களைக் கொண்டுள்ளன; ஒவ்வொன்றும் ஒரு கணம் அல்லது ஒரு வகையைச் சித்தரிக்கிறது. இந்த வடிவங்கள் எவ்வாறு ஒன்றுடன் ஒன்று மேற்கவின்றன என்பதைக் கொண்டு கணங்களுக்கு இடையிலான உறவுகளைக் காட்டுகின்றன. ஒவ்வொரு வளைவும் தளத்தை இரண்டு பகுதிகளாக அல்லது "மண்டலங்களாக"ப் பிரிக்கிறது; வளைவின் உட்புறம், கணத்தின் உறுப்புகளைக் குறிக்கிறது; வெளிப்புறம், அக் கணத்திலமையாத உறுப்புகளையும் குறிக்கிறது. ஒன்றுடன் ஒன்று இணைக்கப்படாத வளைவுகள் பொதுவான கூறுகள் இல்லாத சேர்ப்பிலாக் கணங்களைக் குறிக்கின்றன. ஒன்றுடன் ஒன்று மேற்கவிந்திருக்கும் இரண்டு வளைவுகள், பொதுவான உறுப்புகளைக் கொண்டுள்ள வெட்டும் கணங்களைக் குறிக்கின்றன. இரண்டு வளைவுகளுக்கும் பொதுவான பகுதியானது அவை குறிக்கும் இரு கணங்களுக்கும் பொதுவான உறுப்புகளைக் கொண்ட கணத்தைக் குறிக்கும். ஒரு வளைவுக்குள் முழுவதுமாக உள்ளமைந்த மற்றொரு வளைவானது முந்தைய வளைவு குறிக்கும் கணத்தின் உட்கணத்தைக் குறிக்கிறது.

வென் வரைபடங்கள், ஆய்லர் வரைபடங்களின் கட்டுப்படுத்தப்பட்ட வடிவமாக அமைகின்றன. ஒரு வென் வரைபடம் அதன் n வளைவுகளுக்கு இடையே சாத்தியமான அனைத்து 2ⁿ அனைத்து மேற்கவிந்த மண்டலங்களையும் கொண்டிருக்க வேண்டும்; இம் மண்டலங்கள், அந்த வென் வரைபடத்திலுள்ள உறுப்பு கணங்களின் சேர்க்கை/விலக்கலின் அனைத்து சேர்க்கைகளையும் குறிக்கின்றன. ஆய்லர் படங்களிலிலிருந்து மாறுபட்டு, வென் படங்களில் கணங்களின் பகுதிகளாக அமையாத இடங்கள் கருப்பு வண்ணத்தில் அமைக்கப்படுகின்றன; உறுப்புக்களாக அமைந்திருக்கும் பண்பானது மேற்கவிதல் மூலமாகவும், வண்ணங்கள் மூலமாகவும் காட்டப்படுகின்றன.

ஆய்லர்/வென் வரைபடங்களுக்கு இடையிலான தொடர்பு

சிறிய வென்பட எடுத்துக்காட்டுகள் (இடப்புறம்) - நிழலிட்ட பகுதிகள் வெற்றுக் கணங்கள்; இவை எளிதாக ஆய்லர் படங்களாக (வலது) மாற்றப்படுவதைக் காட்டுகிறது

வென் வரைபடங்கள், ஆய்லர் வரைபடங்களின் கட்டுப்படுத்தப்பட்ட வடிவமாக அமைகின்றன. ஒரு வென் வரைபடம் அதன் n வளைவுகளுக்கு இடையே சாத்தியமான அனைத்து 2ⁿ அனைத்து மேற்கவிந்த மண்டலங்களையும் கொண்டிருக்க வேண்டும்; இம் மண்டலங்கள், அந்த வென் வரைபடத்திலுள்ள உறுப்பு கணங்களின் சேர்க்கை/விலக்கலின் அனைத்து சேர்க்கைகளையும் குறிக்கின்றன. ஆய்லர் படங்களிலிலிருந்து மாறுபட்டு, வென் படங்களில் கணங்களின் பகுதிகளாக அமையாத இடங்கள் கருப்பு வண்ணத்தில் அமைக்கப்படுகின்றன; உறுப்புக்களாக அமைந்திருக்கும் பண்பானது மேற்கவிதல் மூலமாகவும், வண்ணங்கள் மூலமாகவும் காட்டப்படுகின்றன.

எடுத்துக்கொள்ளப்படும் கணங்களின் எண்ணிக்கை மூன்றைத் தாண்டினால், வென் வரைபடங்கள் ஆய்லர் வரைபடங்களைவிடச் சிக்கலானவையாகி விடுகின்றன.

இரு வரைபடங்களுக்குமான வேறுபாட்டை விளக்கும் எடுத்துக்காட்டு:

எடுத்துக்கொள்ளப்படும் கணங்கள்: